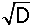
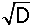
De vierkantsvergelijking
x2 + bx + c = 0
heeft twee oplossingen
x1 en x2 (x1 < x2) en een discriminant D.
Het verschil   x2 − x1 is dan gelijk aan 		A.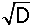  
B.  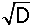 1op2
C.   b
D.   |b|
E.   |c|
A    B    C    D    E

[ 4-3438 - op net sinds 21.10.12-(E)-4.11.2023 ]

Translation in   E N G L I S H

The quadratic equation
x2 + bx + c = 0
has two roots
x1 and x2 (x1 < x2)
and discriminant D.
De difference   x2 − x1   is equal to 		A.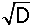  
B.  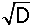1op2
C.  b
D.  |b|
E.  |c|

Oplossing - Solution

De twee oplossingen van een vierkantsvergelijking  ax² + bx + c = 0  worden gegeven door \(\frac {-b+\sqrt D} {2a} \) en \(\frac {-b-\sqrt D} {2a} \).
In ons geval (met a=1) levert dit op : \(\frac {-b+\sqrt D} {2a} > \frac {-b-\sqrt D} {2a} \)
Het positieve verschil is bijgevolg
\(\frac {-b+\sqrt D} {2a}-\frac {-b-\sqrt D} {2a}=\frac{-b+\sqrt D+b+\sqrt D}{2}=\frac{2\sqrt D}{D}=\cdots \)
gricha