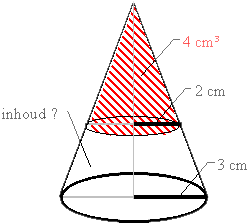
De rode top van deze kegel heeft een inhoud van 4 cm3 (zie figuur)
Als deze wordt weggenomen, wat is dan de inhoud van het overblijvende deel ? (de afgeknotte kegel dus)		 A.   2 cm3
B.   5 cm3
C.   6 cm3
D.   9,5 cm3
E.   13,5 cm3
A    B    C    D    E 

[ 6-3416 - op net sinds 2.2.02-()-30.10.2023 ]

Translation in   E N G L I S H

What is the volume of the truncated cone ?

IN CONSTRUCTION
 A.  
B.  
C.  
D.  
E.  

Oplossing - Solution

Aan de stralen van de cirkels zien we dat het om een gelijkvormigheid van 1,5 gaat, m.a.w. de volledige kegel heeft een inhoud die 1,5³ keer groter is dan het volume van de rode top, 4 cm³ (gegeven)
De volledige kegel heeft dus een inhoud van 1,5³.4 cm³ = 3.3.1,5 cm³ = 13,5 cm³. Trek daar 4 cm³ af en je hebt de inhoud van de afgeknotte kegel.
gricha