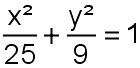 trekt men een verticale rechte die de ellips in het eerste kwadrant snijdt in A.
In dat snijpunt trekt men een raaklijn aan de ellips.
trekt men een verticale rechte die de ellips in het eerste kwadrant snijdt in A.
In dat snijpunt trekt men een raaklijn aan de ellips.Die raaklijn snijdt de x-as in een punt met abscis
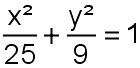 trekt men een verticale rechte die de ellips in het eerste kwadrant snijdt in A.
In dat snijpunt trekt men een raaklijn aan de ellips.
trekt men een verticale rechte die de ellips in het eerste kwadrant snijdt in A.
In dat snijpunt trekt men een raaklijn aan de ellips.Die raaklijn snijdt de x-as in een punt met abscis |
A. 5 |
|---|---|
| B. 6,25 | |
| C. 8 | |
| D. 8,33.. | |
| E. 9 |
[ 6-3279 - op net sinds 8.10.02-(E)-22.6.2025 ]
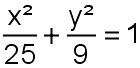 intersects the ellips at a point (A) of the first quadrant.
In that point we draw the tangent line. intersects the ellips at a point (A) of the first quadrant.
In that point we draw the tangent line.That line intersects the x-axis at |
A. 5 |
|---|---|
| B. 6.25 | |
| C. 8 | |
| D. 8.33... | |
| E. 9 |
