en F ' en F zijn de twee brand-punten, dan staan F T en F ' T loodrecht op elkaar als de verhouding
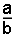 gelijk is aan
gelijk is aan
|
Als T de top is van de ellips met vergelijking
en F ' en F zijn de twee brand-punten, dan staan F T en F ' T loodrecht op elkaar als de verhouding 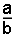 gelijk is aan gelijk is aan
|
A. |
|---|---|
| B. 2 | |
| C. | |
| D. 3 | |
| E. 1,5 |
[ 6-3218 - op net sinds 13.11.03-(E)-22.6.2025 ]
|
(T co-vertex; F and F' foci) F T en F ' T are perpendicular to each other if the fraction 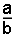 equals equals
|
A. |
|---|---|
| B. 2 | |
| C. | |
| D. 3 | |
| E. 1.5 |
