vierkantsvergelijking
heeft
 en −
en − 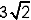
als oplossingen ?
 − 12 = 0
− 12 = 0 − 12 = 0
− 12 = 0 − 12 = 0
− 12 = 0 − 12 = 0
− 12 = 0 ).(x + 2
).(x + 2 ) = 0
) = 0|
Welke vierkantsvergelijking heeft  en − en − 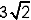 als oplossingen ? |
A. x2 + 5x − 12 = 0 − 12 = 0 |
|---|---|
B. x2 − 5x − 12 = 0 − 12 = 0 | |
C. x2 + x − 12 = 0 − 12 = 0 | |
D. x2 −x − 12 = 0 − 12 = 0 | |
E. (x − 3 ).(x + 2 ).(x + 2 ) = 0 ) = 0 |
[ 4-3148 - op net sinds 15.6.15-(E)-15.7.2024 ]
|
Which equation has  and − and − 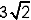 as solutions ? |
A. x2 + 5x − 12 = 0 − 12 = 0 |
|---|---|
B. x2 − 5x − 12 = 0 − 12 = 0 | |
C. x2 + x − 12 = 0 − 12 = 0 | |
D. x2 −x − 12 = 0 − 12 = 0 | |
E. (x − 3 ).(x + 2 ).(x + 2 ) = 0 ) = 0 |