Als men twee van de zes antwoorden willekeurig kiest (gokken dus), wat is dan de kans dat het correcte antwoord zich bevindt onder die twee aangestipte antwoorden ?



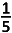
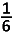
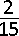
|
Bij een multiple choise test worden per vraag
zes alternatieven/antwoorden gegeven
waarvan er precies één juist is. Als men twee van de zes antwoorden willekeurig kiest (gokken dus), wat is dan de kans dat het correcte antwoord zich bevindt onder die twee aangestipte antwoorden ? |
A.  |
|---|---|
B.  | |
C.  | |
D. 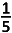 | |
E. 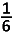 | |
F. 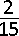 |
[ 6-3088 - op net sinds 5.1.14-(E)-3.11.2023 ]
| IN CONSTRUCTION | A. |
|---|---|
| B. | |
| C. | |
| D. | |
| E. |