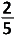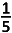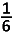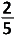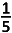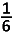Ik gooi drie onvervalste dobbelstenen.
De drie uitslagen zijn verschillend.
Men gooit nu twee dobbelstenen erbij
(zonder de eerste drie te raken).
Wat is de kans dat de vijf
uitslagen verschillend zijn ?
|
A.  |
|---|
B.  |
C. 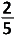 |
D.  |
E. 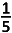 |
F. 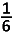 |
[ 6-3078 - op net sinds 7.4.13-()-3.11.2023 ]
Translation in E N G L I S H
|
IN CONSTRUCTION
|
A. |
|---|
| B. |
| C. |
| D. |
| E. |
Oplossing - Solution
1ste manier : gebruik makend van de productwet → P(A∩B) = P(A).P(B|A)
De 5 uitslagen zijn verschillend als de 4de verschillend is van de 3 vorigen en de 5de verschillend is van de 4 vorigen.
Kans dat de 4de verschillend is van de 3 vorigen is 3 op 6.
Kans dat de 5de verschillend is van de 4 vorigen (in de veronderstelling dat de 4de al verschillend was van de 3 vorigen) : 2 op 6.
Dit levert de volgende kans : \(\frac36.\frac26=\frac16 \)
2de manier : met Variaties en de formule van LAPLACE
Twee dobbelstenen hebben 36 (6²) even waarschijnlijke uitkomsten (noemer in de formule van LAPLACE).
De gunstige uitkomsten krijgen we als we 2 getallen kiezen (in volgorde) uit de drie getallen die nog niet gegooid waren : V32 = 3.2 = 6 (teller).
Dit levert ons de kans \(\frac {6} {36}=\frac16 \)