A B O X gricha - v2990 - 23.6.2022
In dit parallellogram,
dat verdeeld is in vier congruente
parallellogrammen, kan de puntvector/plaatsvector xvec
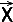
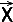geschreven worden als 		A.   \(\frac12\vec A-\vec B\)
B.   \(\frac12\vec B-\vec A\)
C.   \(\vec A +\frac12\vec B\)
D.   \(\frac12\vec B-\frac12\vec A\)
E.   \(-\vec A-\vec B\)
A  B  C  D  E

[ 4-2990 - op net sinds 21.2.15-()-18.7.2024 ]

Translation in   E N G L I S H

A B O X gricha - v2990 - 23.6.2022
IN CONSTRUCTION

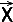xvec = 		A.   \(\frac12\vec A-\vec B\)
B.   \(\frac12\vec B-\vec A\)
C.   \(\vec A +\frac12\vec B\)
D.   \(\frac12\vec B-\frac12\vec A\)
E.   \(-\vec A-\vec B\)

Oplossing - Solution

Gebruik de regel van het parallellogram : \(\overrightarrow{B}=2.\overrightarrow{X}+\overrightarrow{A} \)
Zodoende is   \(2.\overrightarrow{X}=\overrightarrow{B}-\overrightarrow{A}\)  zodat  \(\overrightarrow{X}=\frac12(\overrightarrow{B}-\overrightarrow{A})= ... \)
gricha