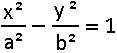
wordt gegeven door
De vergelijking van de raaklijn
in het punt (x1 , y1) van de
hyperbool 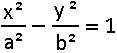 wordt gegeven door |
A. \(\large\boldsymbol{\frac {x_1 x} {a^2}+\frac{y_1 y}{b^2}=1 }\) |
|---|---|
| B. \(\large\boldsymbol{\frac {y_1 y} {b^2}-\frac{x_1 x}{a^2}=1 }\) | |
| C. \(\large\boldsymbol{\frac {x_1 x} {a^2}-\frac{y_1 y}{b^2}=-1 }\) | |
| D. \(\large\boldsymbol{\frac {x_1 x} {a^2}-\frac{y_1 y}{b^2}=1 }\) | |
| E. \(\boldsymbol{\text{geen van de vorige} }\) |
[ 6-2692 - op net sinds 11.1.14-()-(E)-6.11.2023 ]
|
The equation of the tangent line at the point (x1, y1) of the hyperbola 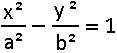 is given by |
A. \(\boldsymbol{\frac {x_1 x} {a^2}+\frac{y_1 y}{b^2}=1 }\) |
|---|---|
| B. \(\boldsymbol{\frac {y_1 y} {b^2}-\frac{x_1 x}{a^2}=1 }\) | |
| C. \(\boldsymbol{\frac {x_1 x} {a^2}-\frac{y_1 y}{b^2}=-1 }\) | |
| D. \(\boldsymbol{\frac {x_1 x} {a^2}-\frac{y_1 y}{b^2}=1 }\) | |
| E. \(\boldsymbol{\text{none of these} }\) |
