de ruimtediagonaal
een hoek α met
een opstaande ribbe.
Hieruit volgt dat

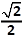
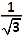
.gif)
|
In een kubus maakt de ruimtediagonaal een hoek α met een opstaande ribbe. Hieruit volgt dat | A. tan α = 1 | |
|---|---|---|
B. tan α =  | ||
C. tan α = 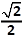 | ||
D. sin α = 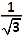 | ||
E. cos α = .gif) |
[ 4-2691 - op net sinds 27.12.2017-(E)-9.11.2024 ]
|
spatial diagonal makes an angle α with an upright edge. Therefore |
A. tan α = 1 |
|---|---|
B. tan α =  | |
C. tan α = 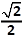 | |
D. sin α = 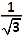 | |
E. cos α = .gif) |