(− x2 + x − 1 ) . x ≥ 0
heeft als oplossingenverzameling
|
De ongelijkheid (− x2 + x − 1 ) . x ≥ 0 heeft als oplossingenverzameling |
A. |
|---|---|
| B. | |
| C. ∅ | |
| D. | |
| E. { 0 } |
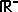 = { x | x ≤ 0 }
= { x | x ≤ 0 } 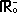 ={ x | x < 0 }
={ x | x < 0 }
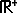 = { x | x ≥ 0 }
= { x | x ≥ 0 }
[ 5-2556 - op net sinds 16.12.04-((E)-16.11.2024 ]
|
The set of solutions of the inequality (− x2 + x − 1 ).x ≥ 0 is |
A. |
|---|---|
| B. | |
| C. ∅ ( empty ) | |
| D. | |
| E. { 0 } ( or x = 0) |