Wiskunde Multiple Choice Vraag uit Gricha's Wiskundige Vragenbank

De limiet van $\frac {x^2+x-12} {x\,-\,3}$ is gelijk aan 0 als	A. x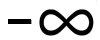
B. x [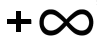
C. x +3
D. x +4
E. x − 4

The limit of $\frac {x^2+x-12} {x\,-\,3}$ is equal to 0 if	A. x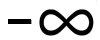
B. x ∞
C. x +3
D. x +4
E. x − 4

$\\A\to\displaystyle\lim_{x\to-\infty}\frac{x^2+x-12}{x\,-\,3}=\lim_{x\to-\infty}\frac{x^2}{x}=\lim_{x\to-\infty}x=-\infty\\B\to\displaystyle\lim_{x\to+\infty}\frac{x^2+x-12}{x\,-\,3}=\lim_{x\to+\infty}\frac{x^2}{x}=\lim_{x\to+\infty}x=+\infty\\C\to\displaystyle\lim_{x\to+3}\frac{x^2+x-12}{x\,-\,3}=\lim_{x\to+3}\frac{(x-3)(x+4)}{x-3}=\lim_{x\to+3}(x+4)=+\infty\\D\to\displaystyle\lim_{x\to+4}\frac{x^2+x-12}{x\,-\,3}=\frac81=8\\E\to\displaystyle\lim_{x\to-4}\frac{x^2+x-12}{x\,-\,3}=\lim_{x\to-4}\frac{(x-3)(x+4)}{x\,-\,3}=\lim_{x\to-4}(x+4)=0$