Voor één bepaalde m-waarde heeft het 2 × 2 stelsel y=4\end{matrix}\right.)
oneindig veel oplossingen.
In dat geval is de oplossingenverzameling |
A. { ( t, t − 2 ) | t ∈  } } |
|---|
B. { ( 2 − t , t ) | t ∈  } } |
C. { ( t, 2 + t ) | t ∈  } } |
D. 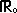 |
E.  2 2 |
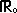 is de verzameling reële getallen zonder nul
is de verzameling reële getallen zonder nul
 2 is de verzameling koppels reële getallen
2 is de verzameling koppels reële getallen
[ 5-2395 - op net sinds 24.7.2020-(E)-27.8.2025 ]
Translation in E N G L I S H
Oplossing - Solution
Een nodige voorwaarde opdat het stelsel \(\small\left\{\begin{matrix} mx-my=2 \\2x+(m-3)y=4\end{matrix}\right. \) oneindig veel
oplossingen zou hebben is dat de determinant van het stelsel 0 is :
\(\small\begin{vmatrix}m&-m\\2&m-3\\\end{vmatrix}=m^2-3m+2m=m(m-1)\)
Deze is 0 voor m = 0 of m = 1.
Voor m = 0 is het stelsel strijdig en heeft het stelsel GEEN oplossingen want dan wordt de eerste vergelijking vals : 0x − 0y = 2.
Het zal dus voor m = 1 zijn dat de vergelijkingen afhankelijk zullen zijn :
x − y = 2 is inderdaad een vergelijking die evenredig is met 2x − 2y = 4.
Alle oplossingen verkrijg je dus door ofwel x te kiezen en y te berekenen, ofwel y te kiezen en x te berekenen (in om het even welke van de twee vergelijkingen).
Kiezen we x = t, dan moet y = t − 2 zijn wat tot koppels van de vorm
( t, t − 2 ) leidt en ons brengt bij alternatief A
 }
} }
} }
} }
} }
} }
} 2 is de verzameling koppels reële getallen
2 is de verzameling koppels reële getallen