Als M het midden is van een zijde van
dit parallellogram dan is 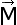 gelijk aan
gelijk aan
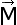 gelijk aan
gelijk aan|
Als M het midden is van een zijde van
dit parallellogram dan is
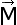 gelijk aan gelijk aan |
A. \(\boldsymbol{\frac 12 \overrightarrow{A}}\) |
|---|---|
| B. \(\boldsymbol{\frac 12 \overrightarrow{B}}\) | |
| C. \(\boldsymbol{\frac 12(\overrightarrow{A}+\overrightarrow{B}) }\) | |
| D. \(\boldsymbol{\frac 12\overrightarrow{B}+\overrightarrow{A} }\) | |
| E. \(\boldsymbol{\frac 12\overrightarrow{A}+\overrightarrow{B} }\) |
[ 4-2362 - op net sinds 1.7.00-(E)-16.7.2024 ]
|
If M het the middle of a side of this parallellogram, then is 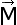 equal to equal to( |
A. \(\boldsymbol{\frac 12 \overrightarrow{A}}\) |
|---|---|
| B. \(\boldsymbol{\frac 12 \overrightarrow{B}}\) | |
| C. \(\boldsymbol{\frac 12(\overrightarrow{A}+\overrightarrow{B}) }\) | |
| D. \(\boldsymbol{\frac 12\overrightarrow{B}+\overrightarrow{A} }\) | |
| E. \(\boldsymbol{\frac 12\overrightarrow{A}+\overrightarrow{B} }\) |
