A B C D E
uit A, B en C
uit A, B en C resp. met hun overstaande zijde
driehoek ABC
driehoek ABC met de zijden
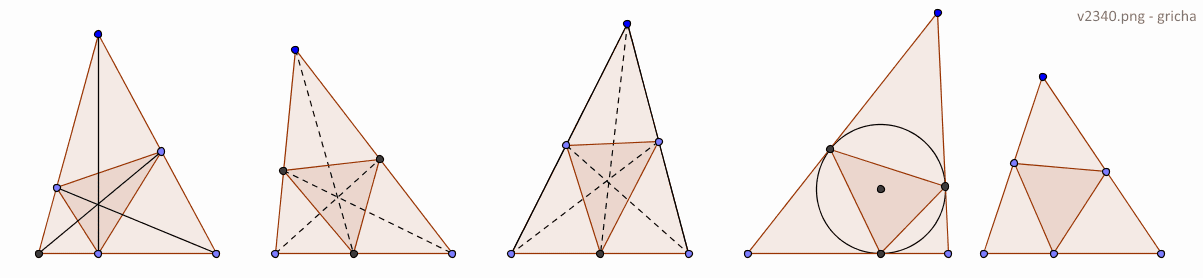
In een scherphoekige driehoek ABC neemt men op elke zijde een punt zodanig dat we een driehoek DEF krijgen. Deze driehoek DEF heeft de kleinste omtrek als de punten D, E en F . . .
 A B C D E |
A. de voetpunten zijn van de hoogtelijnen uit A, B en C |
|---|---|
| B. de snijpunten zijn van de bissectrices uit A, B en C resp. met hun overstaande zijde | |
| C. de middens zijn van de drie zijden van driehoek ABC | |
| D. de raakpunten zijn van de incirkel van driehoek ABC met de zijden | |
| E. een gelijkzijdige driehoek DEF vormen |
[ 3,4,5-2340 - op net sinds 1.11.13-(E)-4.11.2024 ]
| IN CONSTRUCTION |
|---|