wortels van de vierkantsvergelijking
ax2 + bx + c = 0.
De parabool met vgl. y = ax2 + bx + c
heeft dan als symmetrie-as
 s
s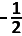 s
s| Weze s = x1 + x2 de som van de wortels van de vierkantsvergelijking ax2 + bx + c = 0. De parabool met vgl. y = ax2 + bx + c heeft dan als symmetrie-as |
A. x = s |
|---|---|
B. x =  s s | |
| C. x = −s | |
D. x = 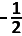 s s | |
| E. x = 2s |
[ 4-2312 - op net sinds 12.4.00-(E)-14.7.2024 ]
|
s = x1+x2 is the sum of the solutions of the quadratic equation ax2 + bx + c = 0. Therefore the parabola with equation y = ax2 + bx + c has axis of symmetry ... |
A. x = s |
|---|---|
| B. x = | |
| C. x = − s | |
| D. x = − | |
| E. x = 2s |
