De oplossingenverzameling van
− x3 + 6x2 − 13x + 10 < 0

is 		A. 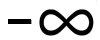  ]minoneindig, 2 [
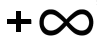B.   ] 2, plusoneindig [
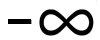C.   ]minoneindig, − 5 [ ∪ ] 1, 2 [
D.   R
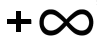E.   ] − 5, −1[ ∪ ] 2, plusoneindig [
A    B    C    D    E 

[ 5-2235 - op net sinds 7.10.15-(E)-29.10.2023 ]

Translation in   E N G L I S H

The solution set of
−x3 + 6x2 − 13x + 10 < 0
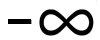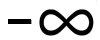is 		A.  ( minoneindig, 2 )
B.  ( 2, ∞ )
C.  ( minoneindig, − 5 ) ∪ ( 1, 2 )
D.  R
E.  ( − 5, −1) ∪ ( 2, ∞ )

Oplossing - Solution

V(x) = −x³ + 6x² − 13x + 10
V(2) = −8 + 24 − 26 + 10 = 0
V(x) is dus deelbaar door x − 2.
Het quotiënt vinden we met de regel van HORNER zodat
V(x) = (x − 2).(−x² + 4x − 5)
Daar de discriminant van de tweede factor D = 16 − 20
negatief is, is (−x² + 4x − 5) steeds negatief en is
(x − 2).(−x² + 4x − 5) < 0 ⇔ (x − 2) > 0 ⇔ x > 2