heeft als
oplossingen-
verzameling
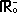 ∪ ] 2, 3 [
∪ ] 2, 3 [|
heeft als oplossingen- verzameling |
A. |
|---|---|
| B. ] 2, | |
| C. ] − 3, 0 [ ∪ ] 2, | |
D. 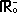 ∪ ] 2, 3 [ ∪ ] 2, 3 [ | |
| E. ] 0, 2 ] ∪ [ 3, |
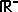 = { x | x ≤ 0 }
= { x | x ≤ 0 }
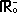 = { x | x ≤ 0 }
= { x | x ≤ 0 }
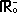 ={ x | x < 0 }
={ x | x < 0 }
[ 5-2102 - op net sinds 5.12.09-(E)-22.8.2025 ]
|
What is the solution set of |
A. 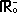 | x <0 |
|---|---|---|
| B. ( 2, ∞) | x >2 | |
| C. ( − 3, 0 ) ∪ ( 2, ∞) | x >2 or -3 <x <0 | |
D. 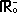 ∪ ( 2, 3 ) ∪ ( 2, 3 ) | x <0 or 2 <x <3 | |
| E. ( 0, 2 ] ∪ [ 3, ∞) | 0 <x ≤ 2 or x ≥ 3 |
