|
Hoever ligt de oorsprong verwijderd van de rechte met vergelijking
x y
— + — = 1 ?
6 8
|
A. 4,5 |
|---|
| B. 4,75 |
| C. 4,8 |
D. 2.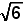 |
| E. 5 |
[ 4-2056 - op net sinds 1.6.2020-(E)-24.10.2023 ]
Translation in E N G L I S H
distance from O to the line
IN CONSTRUCTION
|
|---|
Oplossing - Solution
1ste manier :
De rechte snijdt de x-as in A(6,0) en de y-as in B(0,8).
Merk op : 6 en 8 zijn precies de getallen die in de vergelijking staan.
Daardoor is ΔOAB een rechthoekige driehoek en is de afstand h gelijk aan de lengte van de hoogtelijn uit O (de rechte hoek).
De schuine zijde [AB] heeft een lengte van 10 (6²+8²=10²).
Door de dubbele oppervlakte van de driehoek op twee manieren te schrijven verkrijgen we de gelijkheid 10.h = 6.8 waaruit volgt dat h = . . .
2de manier :
Vermenigvuldig beide leden van de vergelijking met 24 (k.g.v. van 6 en 8).
We verkrijgen : 4x + 3y = 24 ⇔ 4x + 3y − 24 = 0 een vergelijking in de vorm
ax + by + c = 0.
Voor deze vorm bestaat er een formule voor de afstand : een breuk met in de noemer de vierkantswortel van a² + b² en in de teller |ax1 + by1 + c| waarbij (x1,y1) het punt is waarvan we de afstand tot de rechte willen kennen.
In ons geval is die teller |4.0 + 3.0 − 24| = 24 en de noemer de vierkantswortel uit 4² + 3² = 16 + 9 = 25 zodat het antwoord is 24/5 = 48/10 = . . .