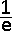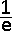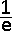De limiet
^x})
is gelijk aan |
A. 0 |
|---|
| B. e |
C. 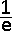 |
| D. 1 |
E. 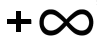 |
[ 6-1801 - op net sinds 10.10.98-(E)-6.11.2024 ]
Translation in E N G L I S H
^x}=)
|
A. 0 |
|---|
| B. e |
C. 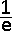 |
| D. 1 |
| E. ∞ |
Oplossing - Solution
\(\displaystyle \lim_{x \to +\infty}\frac{x^x}{(x+1)^x}=\displaystyle \lim_{x \to +\infty}\left (\frac{x}{x+1} \right )^x=\displaystyle \lim_{x \to +\infty}\left (\frac{x+1}{x} \right )^{-x}\\=\displaystyle \lim_{x \to +\infty}\left (1+\frac{1}{x} \right )^{-x}=\frac{1}{\displaystyle \lim_{x \to +\infty}\left (1+\frac{1}{x} \right )^x }= \frac 1e \)