De oplossingen-
verzameling
van
^2\,&space;(x+2)^{13}}{5x}\leqslant&space;0)
is |
A. [ − 2 , 0 [ |
|---|
| B. [ − 2 , 0 [ ∪ { 3 } |
C. [ − 2 , 0 [ ∪ [ 3 , 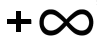 [ [ |
D. 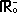 ∪ { 3 } ∪ { 3 } |
| E. ] 0 , 2 ] ∪ { 3 } |
[ 4-1740-1987 - op net sinds 10.7.99-((E)-26.7.2024]
Translation in E N G L I S H
What is the solution set of
^2\,&space;(x+2)^{13}}{5x}\leq&space;&space;0)
|
A. [ −2, 0 ) |
|---|
| B. [ −2, 0 ) ∪ { 3 } |
| C. [ −2, 0 ) ∪ [ 3, ∞ ) |
D. (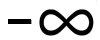 , 0 ) ∪ { 3 } , 0 ) ∪ { 3 } |
| E. ( 0, 2 ] ∪ { 3 } |
Oplossing - Solution
De breuk heeft 3 en − 2 als nulwaarden (WEL oplossing van de ongelijkheid) en 0 als pool (GEEN oplossing van de ongelijkheid).
Om het teken van het eerste lid te bepalen kunnen we met een schema werken maar ook zonder :
Voor de andere getallen kunnen we zowel (3 − x)² als 5 gewoon weglaten.
(x + 2)13 heeft hetzelfde teken als x + 2.
Het teken van het eerste lid wordt dus bepaald door het quotiënt van x +2 door x wat hetzelfde teken is als het product van (x + 2) en x ! !
x.(x + 2) = x² + 2x heeft een negatief teken tussen de nulwaarden, dus in ]− 2,0[
Hier moet nu nog − 2 en 3 worden bijgevoegd zodat de oplossingenverzameling gelijk is aan [− 2,0[ ∪ {3}
>

