Uit de figuur volgt dat
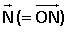 gelijk is aan
gelijk is aan
|
OACB is een parallellogram. Uit de figuur volgt dat 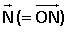 gelijk is aan gelijk is aan
|
A. \(\small\boldsymbol{ \overrightarrow{A}+\frac 12\overrightarrow{B} }\) |
|---|---|
| B. \(\small\boldsymbol{\frac 12\left(\overrightarrow{A}+\frac 12\overrightarrow{B}\right ) }\) | |
| C. \(\small\boldsymbol{\frac 13\left(\overrightarrow{A}+\overrightarrow{B}\right ) }\) | |
| D. \(\small\boldsymbol{\frac 14\left(\overrightarrow{A}+\overrightarrow{B}\right ) }\) | |
| E. \(\small\boldsymbol{\frac 23 \overrightarrow{A} }\) |
[ 4-1270 - op net sinds 31.7.12-(E)-11.11.2023 ]
|
OACB is a parallelogram. From the figure you may conclude that 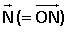 equals equals |
A. \(\small\boldsymbol{ \overrightarrow{A}+\frac 12\overrightarrow{B} }\) |
|---|---|
| B. \(\small\boldsymbol{\frac 12\left(\overrightarrow{A}+\frac 12\overrightarrow{B}\right ) }\) | |
| C. \(\small\boldsymbol{\frac 13\left(\overrightarrow{A}+\overrightarrow{B}\right ) }\) | |
| D. \(\small\boldsymbol{\frac 14\left(\overrightarrow{A}+\overrightarrow{B}\right ) }\) | |
| E. \(\small\boldsymbol{\frac 23 \overrightarrow{A} }\) |
