Het stelsel
\( \left\{\begin{matrix} 2x+y=12\\3x+\frac 32{} = 18 \end{matrix}\right. \)
heeft ( in r2 )
 A.   precies één oplossing
B.   precies twee oplossingen
C.   oneindig veel oplossingen,
maar niet alle koppels reële getallen
D.   oneindig veel oplossingen,
maar wel alle koppels reële getallen
E.   geen oplossingen
A    B    C    D    E 

[ 4-0539 - op net sinds 1.9.12-(E)-3.11.2023 ]

Translation in   E N G L I S H

The system

\( \left\{\begin{matrix} 2x+y=12\\3x+\frac 32{} = 18 \end{matrix}\right. \)

has 		A.  exactly one solution
B.  exactly two solutions
C.  infinity many solutions,
but NOT all the couples of real numbers
D.  infinity many solutions, the set r2
E.  no solutions

Oplossing - Solution

De vergelijkingen zijn afhankelijk : de tweede verkrijg ja na vermenigvuldiging van de eerste met het getal 1,5.
Ze stellen in het xy-vlak dus dezelfde rechten voor !
Er zijn dus oneindig veel oplossingen, maar niet alle koppels reële getallen : bv. (0,0) is GEEN oplossing. Alle oplossingen kunnen weergegeven worden door { (t, 12 − 2t) | t ∈ r.
Omdat er maar één vrijheidsgraad is zegt men soms dat er ∞1 oplossingen zijn, in tegenstelling tot het alternatief D waarbij er twee vrijheidsgraden zijn (x en y mag je dan kiezen) : daar zegt met dan soms dat er ∞² oplossingen zijn
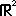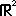gricha