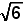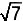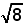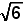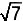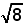Wiskunde Multiple Choice Vraag uit Gricha's Wiskundige Vragenbank

Het middelpunt van het bovenvlak van een kubus met ribbe 2 ligt evenver van de vier hoekpunten van het grondvlak van die kubus. Die afstand is gelijk aan	A.
	B.
	C.
	D.
	E.
	F. 2
	G. 3

[ 5,6-0254 - op net sinds 10.4.98-(E)-16.7.2024 ]

The center of the upper surface of a cube with edge 2, has the same distance to the four corners of the cube. That distance is equal to	A.
	B.
	C.
	D.
	E.
	F. 2
	G. 3

De diagonaal van het grondvlak (een vierkant met zijde 2)
heeft een lengte van 2v2

Weze T' de projectie van de top T op dat grondvlak.
Dan is T'AT een rechthoekige driehoek met |AT'| = v2puur

en |TT'| = 2.
Met de stelling van Pythagoras vinden we vervolgens
|AT|² = |AT'|² + |TT'|² = 2 + 4 = 6
De gevraagde lengte is dan |AT| = ...