Wiskunde Multiple Choice Vraag uit Gricha's Wiskundige Vragenbank

Vind je een fout in de opgave, zelfs een spellingsfout of een layout die beter kan of een figuur die niet doorkomt, of een verkeerde vraag bij een opgave : gelieve mij een lege mail te sturen ( gricha@gricha.be ) met alleen in het onderwerp bv. vraag 9876 nakijken a.u.b. Bedankt !

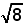
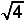
Wat is de grootste afstand tussen twee hoekpunten van een kubus met ribbe 1 (m.a.w. wat is de lengte van de ruimtediagionaal) ?	A.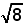
B.
C.
D.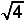
E.

What is the greatest distance between two vertices of a cube with edge 1 ? IN CONSTRUCTION	A.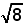
B.
C.
D.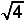
E.

Snij de kubus volgens de diagonaal van een zijvlak in twee gelijke delen. De doorsnede is een rechthoek waarvan de diagonaal de lengte (x) heeft van de ruimtediagonaal (ook lichaamsdiagonaal genoemd). De afmetingen van die rechthoek zijn 1 en v2puur

.
[Het zou parate kennis moeten zijn dat de diagonaal van een vierkant met zijde 1 gelijk is aan v2puur

]
Nu is het voldoende de stelling van Pythagoras toe te passen :
x² = 1² + ( v2puur

)² = 1 + 2 = 3 zodat x =

.
Merk nu op : de lengtes van een ribbe, een zijvlaksdiagonaal en
een lichaamsdiagonaal zijn resp. √1 , √2 en √3