1ste manier :
We gebruiken de formule \(\large\frac {|ux_1+vy_1+w|} {\sqrt{u^2+v^2}} \) om de afstand van (x
1, y
1) tot ux + vy + w = 0 te berekenen :
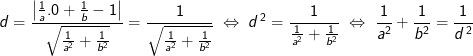2de manier :
De gegeven rechte gaat door de punten A( a, 0 ) en B( 0, b ).
Als a of b negatief zijn kan je altijd de ΔOAB spiegelen zodat de driehoek in het eerste kwadrant ligt, met behoud van de afstand d.
Het schaadt de algemeenheid dus niet als we veronderstellen dat a > 0 en b > 0.
De afstand d is dan de lengte van de hoogtelijn uit O op de schuine zijde van ΔOAB.
De oppervlakte van ΔOAB kan je nu op twee manieren schrijven waardoor de volgende gelijkheid ontstaat :
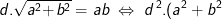=a^2.b^2\;\Leftrightarrow\;\frac{a^2+b^2}{a^2.b^2}=\frac{1}{d^2}\;\Leftrightarrow\;\frac{1}{b^2}+\frac{1}{a^2}=\frac{1}{d^{\,2} "\\d.\sqrt{a^2+b^2}=ab\;\Leftrightarrow\;d^{\,2}.(a^2+b^2)=a^2.b^2\;\Leftrightarrow\;\frac{a^2+b^2}{a^2.b^2}=\frac{1}{d^2}\;\Leftrightarrow\;\frac{1}{b^2}+\frac{1}{a^2}=\frac{1}{d^{\,2}")
