Te bewijzen :   n7 − n   = deelbaar-door-7
m.a.w.   n7 − n   is deelbaar door 7
Bewijs :
Deel I De formule is triviaal voor n = 0 en n = 1. We beginnen dus bij n = 2.
De uitdrukking is dat gelijk aan  27 − 2 = 128 − 2 = 126 = 7.18 = deelbaar-door-7
Deel II Gegeven :   k7 − k   = deelbaar-door-7   ( I.H.)
Te bewijzen:   (k+1)7 − (k+1)   = deelbaar-door-7
Bewijs : LL = (k+1)7 − (k+1) 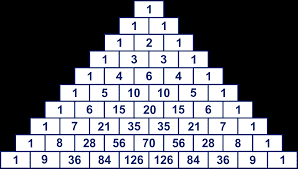driehoekvanPascal
__= k7+7k6+21k5+35k4+35k3+21k2+7k+1 − k−1
__= (k7− k) + 7.(k6 + 3k5 + 5k4 + 5k3 + 3k2 + k)
Beide termen zijn deelbaar door 7, de eerste omwille van de inductiehypothese, de tweede omwille van de factor 7.
De hele som is dus deelbaar door 7   Q.E.D.
N.B. Een bewijs zonder Volledige Inductie is veel sneller gegeven als je de (kleine) stelling van FERMAT kent.
Die zegt dat  ap − a  deelbaar is door p als p een priemgetal is (en a willekeurig natuurlijk getal).
Vermits 7 een priemgetal is, is "n7 − n deelbaar door 7" een direct gevolg van de kleine stelling van FERMAT
Door het principe van volledige inductie is de stelling waar voor n = 2 (Deel I),
n = 3 (Deel II), n = 4 (Deel II), n = 5 ...   m.a.w. voor elk natuurlijk getal n
I.H. = Inductiehypothese     Q.E.D. = quod erat demonstrandum
Deel  I  = BASIC STEP
Deel II = INDUCTIVE STEP