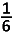 n(2n2 + 9n + 1)
n(2n2 + 9n + 1)LL = 1²+2.1−1 = 1 + 2 − 1 = 2 (de eerste term)
RL =
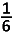 (2+ 9 + 1) = 2
(2+ 9 + 1) = 2LL = RL → O.K.
| Te bewijzen : | 2 + 7 + 14 + 23 + ... + (n2 + 2n − 1) = 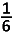 n(2n2 + 9n + 1) n(2n2 + 9n + 1) |
| m.a.w. | |
| Bewijs : | |
| Deel I |
Voor de kleinste n-waarde, nl. 1 is LL = 1²+2.1−1 = 1 + 2 − 1 = 2 (de eerste term) RL = 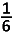 (2+ 9 + 1) = 2 (2+ 9 + 1) = 2LL = RL → O.K. |
| Deel II | Gegeven : |
2 + 7 + 14 + 23 + ... + (k2 + 2k − 1) = 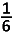 k(2k2 + 9k + 1) ( I.H.) k(2k2 + 9k + 1) ( I.H.)
|
| Te bewijzen: |
2 + 7 + 14 + 23 + ... + (k2 + 2k − 1) + [(k+1)² +2(k+1)−1] = 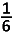 (k+1)[2(k+1)2 + 9(k+1) + 1] (k+1)[2(k+1)2 + 9(k+1) + 1]
| |
| Bewijs : |
We herberekenen eerst het rechterlid : RL = | |
|
LL = | ||
| __
= | ||
| __
= | ||
| __
= | ||
| __
= | ||
| __
= | ||
| __ = RL Q.E.D. |