of : 4n − 1 is een drievoud
of : 4n − 1 is een veelvoud van 3
of :
neem je n = 0, dan is 4n − 1 = 40 − 1 = 0 = 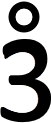
neem je n = 1, dan is 4n − 1 = 41 − 1 = 3 =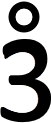
in beide gevallen dus deelbaar door 3neem je n = 1, dan is 4n − 1 = 41 − 1 = 3 =
| Te bewijzen : | 4n − 1 = |
|
of : 4n − 1 is deelbaar door 3 of : 4n − 1 is een drievoud of : 4n − 1 is een veelvoud van 3 of : | |
| Bewijs : | |
| Deel I |
De stelling is waar voor de kleinste n-waarde :
neem je n = 0, dan is 4n − 1 = 40 − 1 = 0 =
in beide gevallen dus deelbaar door 3neem je n = 1, dan is 4n − 1 = 41 − 1 = 3 = |
| Deel II | Gegeven : |
4k − 1 = |
| Te bewijzen: |
4k+1 − 1 = | |
| Bewijs : | 4k+1 − 1 | |
| = 4.4k − 4 + 3 | ||
| = 4.(4k − 1) + 3 | ||
|
(4k − 1) = zodat de twee termen (de hele som) deelbaar is door 3. Q.E.D. |