Bewijs van een stelling door Volledige Inductie (mathematical Induction) : Voorbeeld 33


Te bewijzen : n3 + 6n2 + 2n = deelbaar-door-3
of :  n3 + 6n2 + 2n  is deelbaar door 3
of :  n3 + 6n2 + 2n  is een drievoud
of :  n3 + 6n2 + 2n  is een veelvoud van 3
of :  1/3 (n3 + 6n2 + 2n) is een natuurlijk getal
Bewijs :
Deel I De stelling is waar voor de kleinste n-waarde :
neem je n = 0, dan is n3 + 6n2 + 2n = 0³ + 6.02 + 2.0 = 0 = 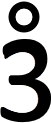deelbaar-door-3
neem je n = 1, dan is n3 + 6n2 + 2n = 1³ + 6.12 + 2.1 = 9 =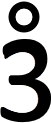 deelbaar-door-3
in beide gevallen dus deelbaar door 3
Nu gaan we bewijzen dat  S( k ) ⇒  S( k+1)
m.a.w. dat als de stelling geldt voor n = k, ze ook zal gelden voor  n = k + 1
Deel II Gegeven : k3 + 6k2 + 2k = deelbaar-door-3     ( I.H.)
Te bewijzen: (k+1)3 + 6(k+1)2 + 2(k+1) = deelbaar-door-3
Bewijs :   (k+1)3 + 6(k+1)2 + 2(k+1)
= k³ + 3k² + 3k + 1 + 6k² + 12k + 6 + 2k + 2
= (k³ + 6k² + 2k) + 3k² + 15k + 9
= (k³ + 6k² + 2k) + 3.(k² + 5k + 3)
De eerste term is deelbaar door 3 omwille van I.H.,
de laatste is een drievoud. De stelling is dus bewezen.
Door het principe van volledige inductie is de stelling waar voor n = 0 (Deel I), n = 1 (Deel I),
n = 2 (Deel II), n = 3 (Deel II) ...   m.a.w. voor elk natuurlijk getal n
I.H. = Inductiehypothese     Q.E.D. = quod erat demonstrandum
Deel  I  = BASIC STEP
Deel II = INDUCTIVE STEP
Nederlands → English→ Français→ Deutsch → Portuguès→ Español
Gegeven Given Donné Gegeben Dado Dado
Te bewijzen To prove A prouver zu beweisen a provar a demostrar
Bewijs Prove Preuve Beweis prova pruebas
voor de kleinste n-waardefor the smallest n-valuepour la plus petite valeur nfür den kleinsten n-Wertpara o valor n mais pequenopara el valor n más pequeño
eerste term first term premier terme der erste Term o primeiro termo primer término
m.a.w. i.e. c'est-à-dire d.h. i.e. es decir
deelbaar door divisible by divisible par teilbar durch divisível por divisible por
even - oneven even - odd pair - impair gerade - ungerade par - impar par - impar
laatste getal last number dernier numéro letzte Zahl último númeroúltimo número
geheel integer entier ganze inteiro entero