De determinant van het stelsel is
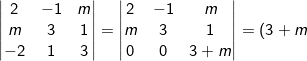(6+m) "\begin{vmatrix}2&-1&m\\m&3&1\\-2&1&3\\\end{vmatrix}=\begin{vmatrix}2&-1&m\\m&3&1\\0&0&3+m\\\end{vmatrix}=(3+m)(6+m)")
Deze wordt 0 voor m = −3 en voor m = − 6
Voor alle andere m-waarden heeft het stelsel precies één oplossing.
Voor m = −3 wordt het stelsel
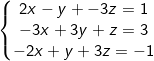
De eerste en de derde vergelijking zijn dezelfde (afhankelijk).
Je kan alle (oneindig vele) oplossingen vinden door z te kiezen en dan x en y te berekenen met bv. de tweede en derde vergelijking.
Voor m = −6 wordt het stelsel
\\-6x+3y+z=3\;\;\quad(2)\\-2x+y+3z=-1\quad(3)\end{matrix}\right. "\left\{\begin{matrix}2x-y+-6z=1\;\quad(1)\\-6x+3y+z=3\;\quad(2)\\-2x+y+3z=-1\quad(3)\end{matrix}\right.")
Als je (1) en (3) optelt krijg je −3z = 0 ⇔ z = 0
Maar voor z = 0 zie je dat (2) en (3) strijdig zijn (
)
Voor m = − 6 zijn er dus geen oplossingen te vinden.
